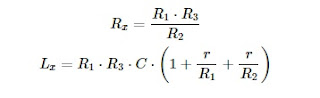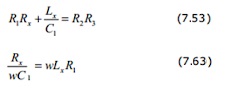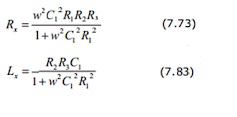PUENTE DE SCHERING

PUENTE DE SCHERING

Es uno de los puentes AC más importantes,  es usado para la medición de capacitores aunque también es muy útil para la medición de algunas propiedades de aislamiento, como ángulos de fase muy cercanos a los 90º.


APLICACIÓN

Mientras que los puentes de Maxwell-Wien, Owen y Hay se emplean para medir inductores, los puentes de Wien y Schering se emplean para medir condensadores. El puente de Schering se emplea sobre todo para medir la fuga en condensadores de alta Tensión.

Para medir capacitores en circuitos donde el ángulo de fase es casi de 90º, el puente de Schering da las lecturas más exactas.


CIRCUITO ELÉCTRICO

FUNCIONAMIENTO

Este tipo de puente tiene la particularidad de medir las fugas de los capacitores en alta tensión, Si queremos obtener información mas precisa sobre la fuga de condensadores, el puente Schering Es el mas indicado debido a que en el Angulo de fase este por encima de 90grados

Sea el circuito mostrado en la siguiente figura:

Para un equilibrio perfecto en este puente, se debe tener en cuenta

Que los nodos A,B,C,D sean efectivamente iguales; es decir, Vab es igual a Vac o Vdb es igual a Vdc y viceversa.

ECUACIONES MATEMÁTICAS

Las ecuaciones de equilibrio se dan de la misma forma que en otros puentes AC,  La ecuación de equilibrio del puente de Schering 

El puente de Schering permite la medida precisa del factor de disipación, 

ω⋅Cx⋅Rx. 

Este puente también se emplea para la medida de los ángulos de pérdida de aislantes y cables para alta tensión. Para realizar esta medida, el nudo que une las ramas donde se encuentran las resistencias R2 y R3 se conecta a tierra.

La deducción de la ecuación de equilibrio del puente de Schering se lleva acabo aplicando el razonamiento expuesto para la deducción de la ecuación de equilibrio del puente de impedancias, esto

es Z1Z2=ZxZ3 con Z1=1j⋅ω⋅C1, Z2=R21+j⋅ω⋅R2⋅C2
 (impedancia equivalente en paralelo de la resistencia R2 y el condensador C2), 
Z3=R3 y Zx=Rx+1j⋅ω⋅Cx

Sustituyendo

1j⋅ω⋅C1R21+j⋅ω⋅R2⋅C2=Rx+1j⋅ω⋅CxR3

Reordenando

1+j⋅ω⋅R2⋅C2j⋅ω⋅R2⋅C1⋅R3=Rx+1j⋅ω⋅Cx

Igualando partes reales e imaginarias se obtiene el valor de Rx y Cx

Rx=R3⋅C2C1Cx=R2⋅C1R3

PUENTE DE ANDERSON

PUENTE DE ANDERSON

Una forma modificada de puente de Maxwell utilizada para la medida de inductancias en términos de capacitancia y resistencia. Dando como ventaja de que ambas condiciones son independientes. El puente posee una resistencia adicional R5. 


APLICACIÓN

se utiliza para la medida de un amplio rango de inductancias con un condesador de capacidad fija. 


CIRCUITO ELÉCTRICO

FUNCIONAMIENTO

El ajuste del puente se lleva a cabo modificando el valor de la resistencia r y de la resistencia conectada en serie, R1, con la impedancia cuyo valor se desea determinar.

La sensibilidad del puente de Anderson se ve favorecida cuando los elementos que componen el puente cumplen

• R1=R2=R32=Rx2
• LxC=2⋅R2x

El puente de Anderson también se emplea para la medida de resistencias residuales mediante el método de sustitución.

ECUACIONES MATEMÁTICAS

La ecuación de equilibrio del puente de Anderson es:

El puente de Anderson también se emplea para la medida de resistencias residuales mediante el método de sustitución.

PUENTE DE HAY

PUENTE DE HAY

Es un circuito puente que generalmente se utiliza para la medida de inductancia en términos de capacitancia, resistencia y frecuencia. Se diferencia del puente Maxwell en que el condensador se dispone en serie con su resistencia asociada.

La configuración de este tipo de puente para medir inductores reales, cuyo modelo circuital consta de una inductancia en serie con una resistencia.


APLICACIÓN

Es Aplicado para la medición de inductancia con respecto a la capacitancia, frecuencia o resistencia, aquí se compara la inductancia con la capacidad. Se utiliza para ángulos de fase grandes en este caso   la resistencia   R1 está en serie con su capacitor   C1,   el valor de R1 debe de ser más bajo que el del capacitor. Este tipo de puente es usado para medición de bobinas o inductores de Q alto.

Este puente se utiliza generalmente para la medida de inductancias en términos de capacitancia, resistencia y frecuencia. La diferencia con el puente de maxwell es que el condensador está en serie con una resistencia.

CIRCUITO ELÉCTRICO

FUNCIONAMIENTO

Es utilizado para la medición de inductancias. Este puente es similar al de maxwell, salvo por el capacitor C1 que se conecta en serie con la resistencia R1, por lo tanto para ángulos de fase grandes la resistencia R1 debe tener un valor muy bajo. Es esta pequeña diferencia constructiva la que permite su utilización para la medición de bobinas de Q alto (Q>10).

ECUACIONES MATEMÁTICAS

Si se sustituyen los valores de impedancias de las ramas del puente en la ecuación

general de equilibrio de los puentes de AC, se obtiene:

Sustituyendo los valores anteriores en la ecuación de equilibrio:

Si se distribuye:

Separando los términos reales de los imaginarios:

Como en ambas ecuaciones (7.53) y (7.63) están presentes los términos  Lx y Rx, se deben resolver simultáneamente, entonces: 

Como se puede observar en las expresiones (7.73) y (7.83) tanto la inductancia como la resistencia desconocida se encuentran en función de la velocidad angular w, por lo tanto sería necesario conocer con exactitud la frecuencia de la fuente de voltaje.

Observando la figura 6:

Se deduce que:

Si los ángulos de fase son iguales, sus tangentes también lo son:

Si se reemplaza (7.93) en las igualdades (7.83), se obtiene:

Para Q>10, el término (1/Q2)<1/100, por lo tanto:

En resumen se puede decir que para la medición de inductores con Q alto (Q>10) se debe utilizar el puente Hay. En el caso de inductores de Q bajo (Q<10) el método apropiado es la medición a través del puente Maxwell. 

VIDEO